問題
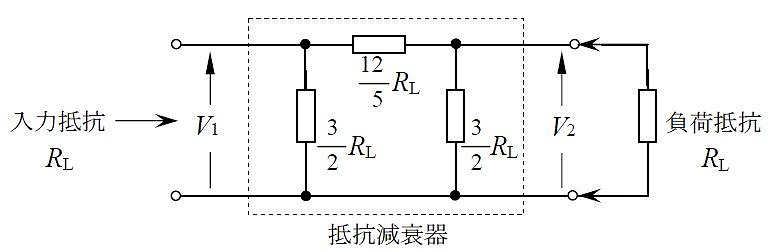
図に示す$\pi$形抵抗減衰器の減衰量$L$の値として、最も近いものを下の番号から選べ。ただし、減衰量$L$は、減衰器の入力電力を$P_1$、入力電力を$V_1$、出力電力を$P_2$、出力電力を$V_2$とすると、次式で表されるものとする。また$\log_{10}2 = 0.3$とする。
$L = 10\log_{10}(P_1 / P_2) = 10\log_{10}{\{(V_1^2 / R_L) / (V_2^2 / R_L)\}}$
| 1 | 3 [dB] |
| 2 | 6 [dB] |
| 3 | 9 [dB] |
| 4 | 14[dB] |
| 5 | 20[dB] |
解答 4
問題からも負荷抵抗は入力抵抗と等しいため、$L$(真数)は以下となる。
$$L = \frac{V_1^2 / R_L}{V_2^2 / R_L} = \frac{V_1^2}{V_2^2}$$
このため、入力電圧$V_1$と出力電圧$V_2$の比がわかればよい。$\frac{3}{2}$$R_L$の並列抵抗$R_1$は次式となる。
$$R_1 = \frac{(3/2)R_L \times R_L}{(3/2)R_L + R_L} = \frac{3}{5}R_L$$
次に、$\frac{12}{5}R_L$と$R_1$の直列抵抗$R_0$は以下となる。
$$R_0 = \frac{12}{5}R_L + \frac{3}{5}R_L = 3R_L$$
よって、$V_2$は以下のようるに表せる。
$$V_2 = \frac{R_1}{R_0}V_1 = \frac{3/5}{3R_L}V_1 = \frac{1}{5}V_1$$
$L$(真数)は、
$$L = \frac{V_1^2}{V_2^2} = 5^2$$
デシベル表示で次のようになる。
$$L = 10\log_{10}5^2 = 20\log_{10}\frac{10}{2} = 20(\log_{10}10 – \log_{10}2) = 20 – 6 =14[dB]$$
