問題
次の記述は、図1及び図2に示す共振回路について述べたものである。このうち誤っているものを下の番号から選べ。ただし、$\omega_0$ は共振角周波数とする。
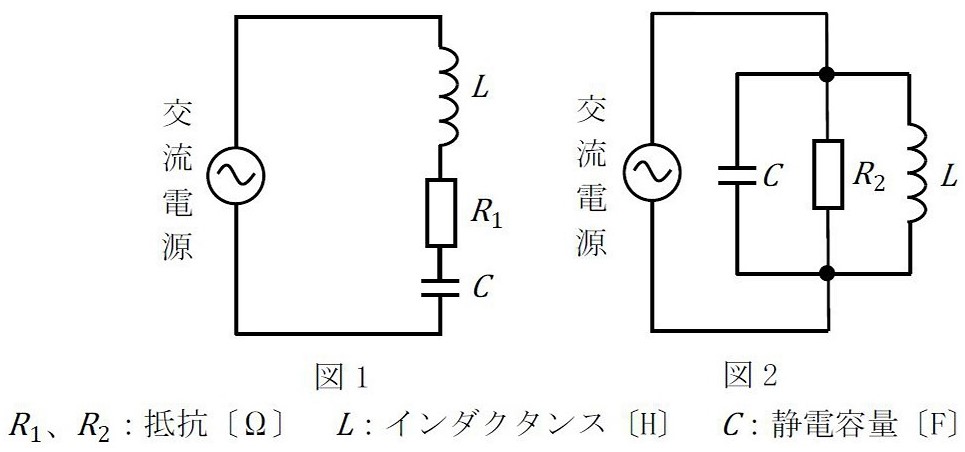
1 図1の共振回路の$Q$ (尖鋭度)は、$Q = \omega_0 CR_1$ である。
2 図1の共振時の回路の合成インピーダンスは、$R_1$ である。
3 図2の共振回路の$Q$ (尖鋭度)は、$Q = \frac{R_2}{\omega_0 L}$ である。
4 図2の共振角周波数$\omega_0$は、$\omega_0 = \frac{1}{\sqrt{LC}}$ である。
解答 1
共振回路
電子回路で使われる共振回路の基本は、LC共振回路です。多数の周波数の中から、希望する周波数を取り出す場合に共振回路が使われます。共振回路の共振の良さを表すのに、$Q$(Quality factor)を使います。$Q$は尖鋭度といいます。共振時に、コイル$L$のリアクタンス$\omega L$とコンデンサ$C$のリアクタンス$1/\omega C$は等しくなります。
$\omega L = \frac{1}{\omega C} より f = \frac{1}{2\pi\sqrt{L C}}$
尖鋭度$Q$は、直列と並列の場合で式が違って、以下のようになります。
【直列共振回路】
$Q = \left|\frac{V_L}{V}\right| または Q = \left|\frac{V_C}{V}\right|$
【並列共振回路】
$Q = \left|\frac{I_L}{I}\right| または Q = \left|\frac{I_C}{I}\right|$
直列共振回路と並列共振回路の$Q$の値は逆数になります。
1 設問図1の直列共振回路では、尖鋭度$Q$は、共振時の電流$\dot{I}$[A]、$R_1$、$L$及び$C$の両端の電圧をおのおの$\dot{V}_{R1}$[V]、$\dot{V}_L$及び$\dot{V}_C$[V]として次のようになる。
$$Q = \frac{|\dot{V}_C|}{|\dot{V}_R1|} = \frac{|j \omega_0 L \dot{I}|}{|R_1 \dot{I}|} = \frac{\omega_0 L}{R_1}$$
また、$|\dot{V}_L| = |\dot{V}_C|$であるから$Q$は次式でも表される。
$$Q = \frac{|\dot{V}_C|}{|\dot{V}_R1|} = \frac{\vert \frac{\dot{I}}{(j \omega_o C) }\vert}{|R_1 \dot{I}|} = \frac{1}{\omega_0 C R_1}$$
設問図2の並列共振回路では、電源電圧を$\dot{V}$[V]、$R_2$、$L$及び$C$に流れる電流をおのおの$\dot{I}_{R2}$[V]、$\dot{I}_L$及び$\dot{I}_C$[V]とすると、次式が成り立つ。
$$\dot{V} = R_2 \dot{I}_{R2}$$
$$\dot{I}_L = \frac{\dot{V}}{j \omega_0 L} = \frac{R_2}{j \omega_0 L} \cdot \dot{I}_{R2}$$
$$\dot{I}_C = j \omega_0 C \dot{V} = j \omega_0 C R_2 \dot{I}_{R2}$$
したがって、直列共振と同様に$Q$は以下のようになる。
$$Q = \frac{|\dot{I}_L|}{|\dot{I}_{R2}|} = \frac{R_2}{\omega_0 L}$$
または、
$$Q = \frac{|\dot{I}_C|}{|\dot{I}_{R2}|} = \omega_0 C R_2$$
