問題
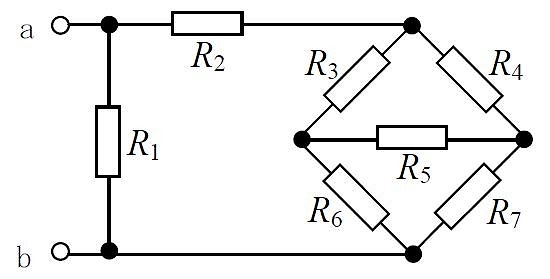
図に示す回路において、端子ab間の合成抵抗の値が20[$\Omega$] であるとき、抵抗$R_1$ の値として、正しいものを下の番号から選べ。ただし、$R_2 = 54[\Omega]$、 $R_3 = 18[\Omega]$、 $R_4 = 6[\Omega]$ 、 $R_5 = 4[\Omega]$、$R_6 = 6[\Omega]$、 $R_7 = 2[\Omega]$ とする。
1 22[$\Omega$]
2 25[$\Omega$]
3 30[$\Omega$]
4 35[$\Omega$]
5 40[$\Omega$]
解答 3
$R_3 \times R_7 = 18 \times 2 = 36[\Omega]$。$R_4 \times R_6 = 6 \times 6 = 36[\Omega]$であるため、回路は$R_5$がブリッジとなるブリッジ回路である。$R_5$の両端は等電位であって切り離すことができる。したがって、ブリッジ回路は、$R_{36} = R_3 + R_6 = 18 + 6 =24[\Omega]$と$R_{47} = R_4 + R_7 = 6 + 2 = 8[\Omega]$の並列合成抵抗$R_{3467} = (R_{36} \times R_{47})/(R_{36} + R_{47}) = (24 \times 8)/(24 + 8) = 6[\Omega]$となる。よって、
$$\frac{R_1(R_2 + R_{3467})}{R_1 + R_2 + R_{3467}} = \frac{R_1 \times 60}{R_1 + 60} = 20[\Omega]より、$$
$R_1 = 30[\Omega]$となる。
