問題
図に示す理想的な演算増幅器（オペアンプ）を使用した反転増幅回路の電圧利得の値として、最も近いものを下の番号から選べ。ただし、図の増幅回路の電圧増幅度$A_V$（真数）は、次式で表されるものとする。また、$\log_{10} 2 = 0.3$ とする。
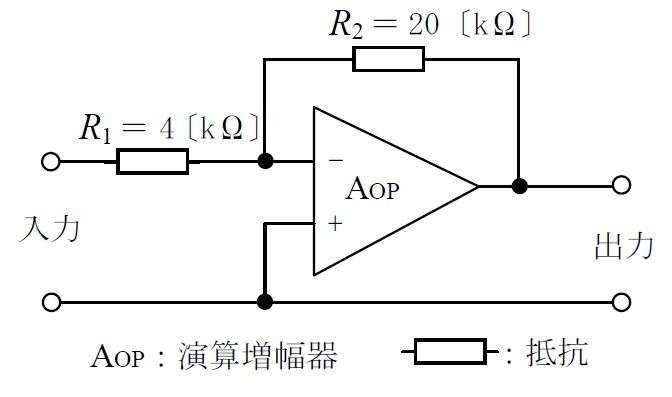
$$A_V = \frac{R_2}{R_1}$$
１ ６[dB]
２ １４[dB]
３ １８[dB]
４ ２４[dB]
５ ２８[dB]
解答 ２
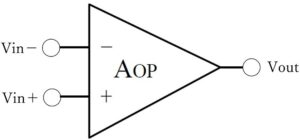理想来なオペアンプの特徴
①入力インピーダンス∞
②出力インピーダンス０
③電圧増幅率∞
入力インピーダンスが∞ということは、入力側に電流が流れないことになります。したがって、$V_{in}－$と$V_{in}＋$に電流は流れませんので、両端子は同電位となります。このことをバーチャルショート（仮想短絡）といいます。問題を解く上では、非常に重要です。また、$V_{in}－$と$V_{in}＋$のどちらかが接地されている場合、他方も同電位ですので接地されているかのような状態になります。このことをイマジナリーアース（仮想接地）といいます。
設問図の反転増幅回路の電圧と電流を下図のように決めれば、入力電圧$V_i$[V]、出力電圧$V_o$[V]は、入力電流$I_i$[A]、出力電流$I_o$[A]、入力抵抗$R_1$[$\Omega$]、帰還抵抗$R_2$[$\Omega$]との間に次の関係がある。
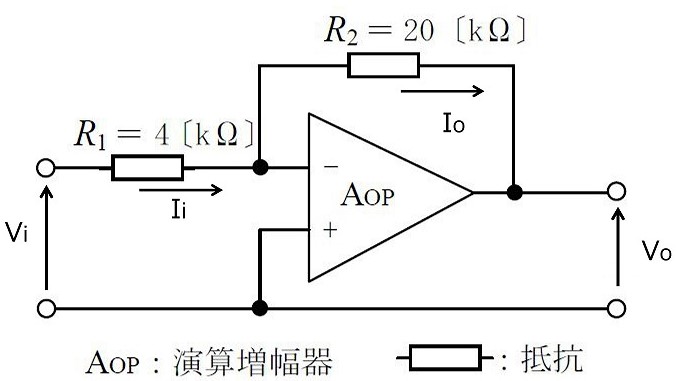
$$V_i = R_1 I_i$$
$$V_o = -R_2I_o$$
上式と$I_i = I_o$の関係から、増幅回路の電圧増幅度Aは、
$$A = \frac{V_o}{V_i} = -\frac{R_2}{R_1}$$
となり、電圧利得Gは、題意の数値を用いて以下のようになる。
$$G = | A | = \frac{R_2}{R_1} = \frac{20 \times 10^3}{4 \times 10^3} = 5$$
デシベル表示で、
$$ 20 \times \log_{10}5 = 20 \times \log_{10}\frac{10}{2} \fallingdotseq 20 \times (1-0.3) = 14 [dB]$$
である。